User:DukeEgr93/Lab 7
This page provides guidance for Labs 6 and 7 for Controls in Summer 2021. It assumes knowledge of SISOtool and Root Locus design as given by User:DukeEgr93/RL Example and Chapter 9 of Nise 8e.
Contents
Introduction
For this part of the lab, you will end up designing and simulating a PD controller for a marginally stable plant and a lead controller for an inherently unstable plant. The plants themselves will be built using passive elements and operational amplifiers. In your report, you will be discussing how well your designs satisfy the criteria given for the system based on both the mathematically simulated results and the circuit simulations.
Building The Plants
The plants for this lab will be second plants with two poles and no zeros. The first plant will be marginally stable with poles at $$\pm j2$$ and the second will be unstable with poles at $$\pm 2$$. The gain in each case will be 4, meaning:
These transfer functions are easy enough to simulate in MATLAB, but you will also be building circuits to simulate them. Unstable circuits generally require some kind of amplification and some kind of feedback. For this lab, the plant will consist of two pure integrators cascaded together (creating a double pole at the origin) along with a difference amplifier (to provide a feedback loop) and a voltage controlled voltage source to adjust the value of $$K$$. Build the following in multisim:

For the capacitors, select each and set their initial conditions to 0 through the Item dialog block (click on a capacitor, then click on the gear at top right if the Item block is not open). For the document, select the Initial conditions section and change the dropdown box to User defined. Set the transient to graph for 5 seconds. If the graphs are too blocky, you can set the Document->Simulation Settings -> Maximum time step to a Manual time step of 1e-5 seconds (the fastest manual time step). It will take some...ahem...time to make the graph but it will be smoother.
- With the gain $$K$$ set to 4 V/V, make a graph with the five probed signals. Save this graph and rename it StepResponse1.
- With the gain $$K$$ set to -4 V/V, make a graph with the five probed signals. Save this graph and rename it StepResponse2.
- Confirm for yourself that the first response is typical of a marginally stable system with a frequency of 2 rad/s and the second response is typical of an unstable system (until the op-amp voltages saturate at 12V for the Probe 4 and 5 readings.
PD Control for Marginal System
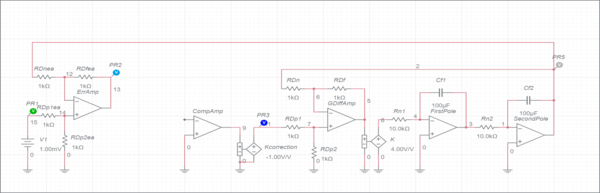
You will now design a compensator to make the system response satisfy particular design criteria. Specifically, you will want a settling time of 0.1 sec and a %OS of 1%. Use SISOtool to figure out what a PD controller would look like for the marginally stable system (where $$K=4$$) and then look at the step response simulation. Take a screen shot of that step response, then build an active PD controller in multisim. The basic circuit you will be working with to control the plant is:
where your compensator will be built on the CompAmp amplifier.
Set V1 to 1 mV, the Kcorrection value to -1 and the K value to +4 V/V. This will allow you to get a step response for a step of 1 mV for the initially marginally stable system. In your graph, choose a time scale that shows how the system responds to the step. You will be comparing this to the numerically simulated response from SISOtool. Remember, if your graph is blocky you may need to manually set the maximum time step for the document to 1e-5. Save the graph as MarginalPlot1 and then turn off the Probe 3 voltage, manually change the vertical scale to focus on the input (probe 1), error (probe 2), and output (probe 5), and save the graph as MarginalPlot2. Save this schematic as MarginalPD and save an image of it.
Next, turn Probe 3 back on a scale to see all the probes. Go back to the schematic, change V1 to 1 V and re-run the simulation. Once again choose a time scale you believe shows all the interesting parts of the response (1 sec works well). Save this graph - this shows what happens when the controller saturates - as MarginalPlot3
PD Control for Unstable System
Go back to SISOtool and replace G with the system where $$K=-4$$. Design a PD compensator for the same design points as above. Take a screen shot of the step response. Make sure you saved the schematic from before, then save it as UnstablePD. You will also need change Kcorrection to 1 and K to -4 to generate the unstable plant. You will be following the same steps as given above:
Set the V1 value to 1 mV. In your graph, choose a time scale that shows how the system responds to the step. You will be comparing this to the numerically simulated response from SISOtool. Remember, if your graph is blocky you may need to manually set the maximum time step for the document to 1e-5. Save the graph as UnstablePDPlot1 and then turn off the Probe 3 voltage, manually change the vertical scale to focus on the input (probe 1), error (probe 2), and output (probe 5), and save the graph as UnstablePDPlot2. Make sure the schematic is called UnstablePD and save an image of it.
Next, turn Probe 3 back on a scale to see all the probes. Go back to the schematic, change V1 to 1 V and re-run the simulation. Once again choose a time scale you believe shows all the interesting parts of the response (1 sec works well). Save this graph as UnstablePDPlot3 - this shows what happens when the controller saturates.
Lead Control for Unstable System
Finally, design a lead controller for the same design criteria. In this case, move the compensator zero to -2 to cancel out one of the system poles. Figure out where the lead pole has to go accordingly. Take a screen shot of the step response. Make sure you saved the schematic from before, then save it as UnstableLead. Kcorrection should still be 1 and K should still be -4 to generate the unstable plant. You will be following the same steps as given above:
Set the V1 value to 1 mV. In your graph, choose a time scale that shows how the system responds to the step. You will be comparing this to the numerically simulated response from SISOtool. Remember, if your graph is blocky you may need to manually set the maximum time step for the document to 1e-5. Save the graph as UnstableLeadPlot1 and then turn off the Probe 3 voltage, manually change the vertical scale to focus on the input (probe 1), error (probe 2), and output (probe 5), and save the graph as UnstableLeadPlot2. Make sure the schematic is called UnstableLead and save an image of it.
Next, turn Probe 3 back on a scale to see all the probes. Go back to the schematic, change V1 to 1 V and re-run the simulation. Once again choose a time scale you believe shows all the interesting parts of the response (1 sec works well). Save this graph as UnstableLeadPlot3 - this shows what happens when the controller saturates.
Lab Report
- For Lab 6, you will upload the Maple worksheet (PDF) that solves 6.3.1 and 6.3.2. The worksheet should include a statement about what the system type is, the value of the static error constant as a function of K_P, and the steady-state error as a function of K_P.
- For Lab 7, you will include the following:
- Your graph StepResponse1 from Building The Plants
- Your graph StepResponse2 from Building The Plants
- Your schematic for PD Control Marginal System
- Your SISOtool screen with design criteria in place and poles at the design point
- In the body of the lab report, include the desired pole locations and the transfer function for the compensator
- Your transient graph MarginalPlot1 from PD Control for Marginal System
- Your transient graph MarginalPlot2 from PD Control for Marginal System
- Your transient graph MarginalPlot3 from PD Control for Marginal System
- Your schematic from PD Control for Unstable System
- Your SISOtool screen with design criteria in place and poles at the design point
- In the body of the lab report, include the desired pole locations (same as above) and the transfer function for the compensator
- Your transient graph UnstablePDPlot1 from PD Control for Unstable System
- Your transient graph UnstablePDPlot2 from PD Control for Unstable System
- Your transient graph UnstablePDPlot3 from PD Control for Unstable System
- Your schematic from Lead Control for Unstable System
- Your SISOtool screen with design criteria in place and poles at the design point
- In the body of the lab report, include the desired pole locations (same as above) and the transfer function for the compensator
- Your transient graph UnstableLeadPlot1 from Lead Control for Unstable System
- Your transient graph UnstableLeadPlot2 from Lead Control for Unstable System
- Your transient graph UnstableLeadPlot3 from Lead Control for Unstable System